Hva er situasjonen?
Vi har et sort hull. Vi har en planet som g?r i bane rundt dette sorte hullet, med en baneradius p? 1 AU (1 AU er den gjennomsnittlige avstanden mellom jorda og sola). Rett ved planeten er det en satellitt. Satellitten beveger seg ikke relativt til planeten. Ombord i denne satellitten sitter jeg. Jeg sender ut r?de lyssignaler ved et bestemt tidsintervall (hvert 59,9925. sekund). Min venn Wen sitter i et romskip som er i fritt fall radielt inn mot sentrum av det sorte hullet. Idet romskipet passerer satellitten min, har det farten v. Wen sender ut bl? lyssignaler hvert 29,2871. sekund (i hans eget referansesystem). Det sorte hullet har en masse p? \(1.75247\cdot10^7 M_{\odot}\). Romskipets "skall-fart" (farten jeg m?ler at det har) idet det fyker forbi meg ved 1 AU fra det sorte hullet er \(v_{shell} = 0.177c\). Under har jeg skissert situasjonen:

OBS! I dette innlegget tar vi ikke hensyn til tiden lyset bruker p? ? reise fra legemene til kameraet. I praksis ville dette betydd at lyset reiste med uendelig hastighet, noe som ikke er mulig. Men fortvil ikke. Dette skal vi ta hensyn til i neste innlegg, s? da f?r vi se hvor stort utslag denne antagelsen faktisk gj?r!
Husker du hvordan vi definerte de ulike typene observat?rer n?r vi holder p? med relativitetsteori? Hvis ikke, ta en oppfriskning her. N? er du klar for dette sp?rsm?let: Hva slags type observat?r vil jeg og Wen v?re? Det kommer nok ikke som en overraskelse at Wen vil v?re den fritt-fallende-observat?ren. Han faller fritt mot gravitasjonssentret i det sorte hullet. I korte tidsintervaller vil han ha tiln?rmet konstant fart, og akselerer ikke. Derfor vil han v?re i et lokalt inertialsystem (forklaring), og han opplever at det er flat romtid. Dermed kan han i korte tidsintervaller bruke vanlig Lorentzgeometri for ? beskrive tidrommet, slik som vi gjorde n?r vi hadde spesiell relativitet. Hva slags observat?r vil jeg v?re, mon tro? Jeg sitter i en satellitt rett utenfor en planet som jeg beveger meg sammen med, og planeten g?r i bane rundt det sorte hullet. Vi g?r i bane et godt stykke utenfor eventhorisonten. Jeg p?virkes av gravitasjonen til det sorte hullet. Jeg vil v?re en skall-observat?r.
Hvordan vil da lyssignalene Wen sender ut se ut for meg? Og vil jeg observere dem momentant idet han sender dem ut? Og hvordan vil han observere mine lyssignaler idet han kommer n?rmere og n?rmere det sorte hullet? For ? finne ut av dette trenger vi noen verkt?y.
Back to the drawing board
Vi kan starte med ? finne en relasjon med hvordan tiden forl?per i v?re respektive referansesystemer. Vi kan da ta utgangspunkt i definisjonen av relativistisk energi i et gravitasjonsfelt:
\(\frac{E}{m} = (1-\frac{2M}{r})\cdot \frac{dt}{d\tau}\) (1)
Her er \(\frac{E}{m}\) energi per masse for raketten, M er massen til det sorte hullet, og r er avstanden mellom raketten og det sorte hullet. dt er et lite tidsintervall for en langt-vekk-observat?r, mens \(d\tau\) er egentiden til raketten. Men vi har ikke en langt-vekk-observat?r... Da m? vi ogs? finne sammenhengen mellom langt-vekk-observat?rens observerte tid, og den tilsvarende tida for en skallobservat?r (alts? meg). Vi kan utlede relasjonen \(\frac{dt}{dt_{shell}}=\frac{1}{\sqrt{1-\frac{2M}{r}}}\) (2), der dt gjelder for langt-vekk-observat?ren, og \(dt_{shell}\) gjelder for skall-observat?ren, og de andre variablene er de samme som tidligere. Her har vi brukt fysiker-matte og skrevet om alle \(\Delta\) til d. S? f?r vi behov for relasjonen mellom tid for alle de tre observat?rene, og i denne setter vi inn uttrykk (2):
\( \frac{dt}{d\tau} =\frac{1}{\sqrt{1-\frac{2M}{r}}}\cdot \frac{dt_{shell}}{d\tau} \) (3)
Til slutt f?r vi da at energien per masse for raketten blir:
\( \frac{E}{m} =\sqrt{1-\frac{2M}{r}}\cdot \frac{dt_{shell}}{d\tau} \) (4)
Her har vi f?tt et uttrykk for hvordan jeg (skall-obs.) og Wen (fritt-fall-obs.) vil oppleve at tiden g?r i forhold til hverandre. Siden vi vet at energi per masse vil v?re konstant for raketten, kan vi se at det eneste dette forholdet varierer med, er avstanden r raketten har til det sorte hullet!
Vi l?ner litt spesiell relativitetsteori
Vi husker at en skall-observat?r, meg i dette tilfellet, kan bruke spesiell relativitet for korte tidsintervaller. Det er fordi om noe skjer i n?rheten av meg over kort tid, vil jeg ikke merke noe til krumningen av romtiden. Man kan sammenlikne dette med det kjente eksemplet man ofte kommer borti n?r man leser om spesiell relativitet - et tog som passerer en observat?r p? bakken. Jordkloden er rund, og derfor er strekningen toget beveger seg over litt krummet. Men, en observat?r p? bakken vil jo se at bakken framfor seg er flat. Han kan bruke Lorentzgeometri. I tillegg vil ikke toget ha konstant fart over hele strekningen den kj?rer. Men observat?ren vil ikke se toget lenge nok til ? observere noen akselerasjon. Derfor trenger ikke observat?ren ? forholde seg til noe annet enn den spesielle relativitetsteorien. Det samme prinsippet gjelder alts? ogs? for meg. ?yeblikket romskipet til Wen passerer meg er kort, s? derfor kan vi skrive om uttrykket for energi per masse om til:
\(\frac{E}{m}= \sqrt{1-\frac{2M}{r}} \cdot \gamma_{shell}\) (5)
der vi har brukt vanlig tidsdilatasjon fra den spesielle relativitetsteorien, der \(\gamma_{shell} = \frac{1}{\sqrt{1-v_{shell}^2}}\). Her er \(v_{shell}\) en lokalt observert skall-fart i en avstand r fra det sorte hullet. Og vipps har vi alle verkt?yene vi trenger for ? kunne forutse hva som vil skje i denne situasjonen. S? la oss gj?re det.
Vi finner Wens avstand til det sorte hullet
Siden tidsintervallet mellom hvert lyssignal Wen og jeg sender ut er s?pass korte (hhv. 29,2871 og 59,9925 sek.) at avstanden mellom romskipet hans og det sorte hullet er tiln?rmet konstant i l?pet av denne tiden. Vent n? litt! Hvis jeg bruker uttrykk (4), kan jeg da finne ut hvor langt unna Wen er det sorte hullet! Energi per masse for raketten er konstant, og egentiden til Wen er konstant. Det eneste jeg trenger ? gj?re er ? m?le tiden mellom to lyssignaler han sender meg. La oss pr?ve dette. F?rst trenger vi ? finne en tallverdi for energi per masse for raketten. Det absolutt enkleste er ? finne ut hva denne er akkurat idet Wens romskip farer forbi satellitten min. Da veit vi hva r er, den er 1 AU. I tillegg har vi m?lt at \(v_{shell} = 0.177\). Massen til det sorte hullet kjente vi til, s? da er det bare ? sette inn disse tallene i uttrykk (5). Da finner vi at \(\frac{E}{m} ≈ 0.83\). Dersom raketten til Wen hadde hatt spinn, ville det betydd at han ville g?tt i bane rundt det sorte hullet. Men siden han kun har fart radielt inn mot det sorte hullet, har den ikke spinn, og kan derfor ikke g? i bane. Wen kommer beklageligvis til ? absorberes av det sorte hullet.
Jeg observerer at det f?rste lyssignalet fra Wen kommer umiddelbart, alts? akkurat samtidig som Wen sender det ut. Husk at vi ikke tar hensyn til tiden lyset bruker p? ? n? fram til meg. Det neste lyssignalet hans kommer etter 30,0208 sekunder p? klokka mi. Hmm, det tok alts? bittelitt lenger tid for meg mellom de to signalene enn for Wen. Men ikke mye. Det gir mening, vi antok at avstanden fra Wens romskip til det sorte hullet var konstant i l?pet av denne tiden. I teorien burde Wen og jeg da m?lt n?yaktig lik tid mellom lyssignalene. Men fordi dette er en tiln?rming, er det ikke s? rart at tidene vil avvike noe. Mellom de to siste lyssignalene, m?ler jeg at det g?r 346,91 sekunder. Da finner vi disse sammenhengene:
| Tid jeg m?ler mellom Wens lyssignaler | Avstand mellom Wens romskip og sort hull | ||
|---|---|---|---|
| Mellom 1. og 2. signal: | 30,0208 sekunder | r = 0.968 AU | r = \(2.80 \cdot 2M\) |
| Mellom 30. og 31. signal: | 346,91 sekunder | r = 0.348 AU | r = \(1.01 \cdot 2M\) |
Vi ser fra tabellen at n?r vi bruker tiden mellom de to f?rste lyssignalene, s? finner vi at raketten til Wen er 0.968 AU (alts? nesten 1AU) unna det sorte hullet. Det gir mening, det er jo m?lt omtrent samtidig som han er p? vei forbi oss. Og vi er i en avstand p? 1AU fra det sorte hullet. N?r vi bruker tiden mellom de to siste lyssignalene, finner vi at han er i en avstand 0.348 AU fra det sorte hullet. Akkurat denne verdien er ikke s? intuitiv for oss. Men vi kan se helt til h?yre i tabellen. Der har vi oppgitt avstandene i Schwarzschild-radius i stedet. Vi ser da at den siste avstanden er p? \(r = 1.01 \cdot 2M\). Alts? er han nesten akkurat ved Schwarzschild-radien, som er p? \(r=2M\). Det m? bety at Wen er rett utenfor eventhorisonten, idet han sender de siste lyssignalene sine til meg. Shit!
Fargene vi ser
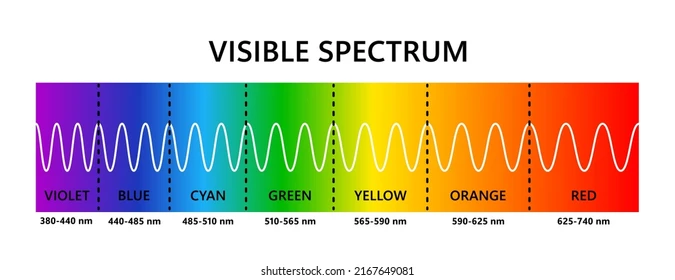
Jeg ser at n?r Wen n?rmer seg det sorte hullet mer og mer, s? skjer det noe interessant med lyssignalene hans. I starten er de bl?-lilla, s? kommer et klart bl?tt lyssignal, og s? er resten av dem r?de. Lyset Wen sender ut blir r?dforskj?vet p? vei til meg! Jeg vil se lys i farger med st?rre b?lgelengde enn lyset Wen sendte ut. Du kan se i figuren til h?yre hva slags b?lgelengde de ulike fargene har.
Siden jeg er en skall-observat?r, vil jeg se at Wen f?r st?rre fart jo n?rmere han kommer det sorte hullet. N?r han er ved eventhorisonten vet jeg at jeg vil observere at han beveger seg med lysfarten! Vi har uttrykket for frekvens:
\(f = f_0 \cdot (1 + \frac{\Delta v}{c})\)
Her er f frekvensen jeg observerer at lyset har, \(f_0\) er frekvensen p? lyset Wen sendte ut, c er lysfarten, og \(\Delta v\) er den negative av farten min minus farten til Wen. Vi definerer positiv retning ut fra det sorte hullet. Da har Wen en negativ fart. Da blir \(\Delta v\) negativ, og vi f?r at \(f < f_0\). Det betyr at jeg vil se lys med lavere frekvens enn lyset Wen sendte ut. Dette stemmer overens med at jeg observerer lys med lengre b?lgelengde.

Av: Jostein Riiser Kristiansen
R?dforskyvningen kommer av at lyset absorberes lenger opp i gravitasjonsfeltet enn de ble sendt ut ved. Man kan tenke seg gravitasjonsfeltet som en trakt. Wen er lenger ned i trakta enn meg, og lyset han sender ut m? bevege seg langs med traktformen opp til meg. Man kan se for seg at lyset da blir strukket langs trakta, og vil derfor ha en lengre b?lgelengde n?r det kommer fram til meg. Det er som om det sorte hullet "holder igjen" alt rundt seg som pr?ver ? reise utover.
Hvordan vil mine lyssignaler se ut for Wen? Jeg ser for meg at det motsatte vil skje hos Wen. Siden jeg sender lyssignaler inn mot det sorte hullet, ser jeg for meg at det sorte hullet vil "trekke dem til seg". Derfor tror jeg at Wen vil se lys med kortere b?lgelengde. Siden jeg sender ut r?de lyssignaler, vil Wen oppleve at de bl?forskyves. Vi kan se p? uttrykket for frekvens igjen. N? er Wen mottageren, s? \(\Delta v\) blir positiv, og vi f?r at \(f > f_0\). Wen vil observere at lyset jeg sendte mot han har f?tt en h?yere frekvens. Det m? bety at han ser lys med kortere b?lgelengder!
Tid og fart
Noe jeg ikke har kommentert p? enda, er at jeg ogs? observerer at lyssignalene til Wen etterhvert kommer med st?rre og st?rre mellomrom. I hvilket tempo kommer mine lyssignal fram til Wen, mon tro? Vi kan se dette fra uttrykk (4). Flytter vi litt rundt p? leddene i den, f?r vi at:
\(d\tau = \frac{\sqrt{1-\frac{2M}{r}}}{E/m} \cdot dt_{shell}\) (6)
Vi ser at n?r Wen kommer n?rmere det sorte hullet (r minker), s? vil egentiden hans mellom to eventer bli en mindre faktor ganget med tiden jeg m?ler mellom eventene. S? Wen vil etterhvert observere at det tar kortere tid mellom hvert lyssignal jeg sender ham. Selv om jeg mener at de sendes ut i et fast intervall!
Likning (5) kan skrives om p? formen:
\(v_{shell} = \sqrt{1 - \frac{1-\frac{2M}{r}}{(E/m)^2}}\)
Fra denne ser vi at jo n?rmere Wen kommer det sorte hullet (r minker), jo st?rre fart vil jeg observere at han har! N?r \(r = 2M\), er Wen p? eventhorisonten, og jeg vil observere at han farten \(v_{shell} = 1\), som er lysfarten! Dette stemmer overens med teorien om hvordan skall-observat?rer observerer farten til legemer i fritt fall inn mot sorte hull.
Hva ser Wen?
N? er det nok synsing, la oss h?re med Wen hva han faktisk observerer. Han sier:
"Jeg vet at du har sendt ut 31 r?de lyssignaler, men jeg ser bare at de f?rste 12 er r?de. Jeg ser deretter ett gult, ett gr?nt, ett bl?tt, og s? er resten av dem lilla. De siste lyssignalene dine kommer fryktelig tett, s? tett at jeg nesten ikke kan se hvor det ene slutter og det neste starter." - Wen
Da er det alts? slik jeg trodde, han ser at lyssignalene mine bl?forskyves. I tillegg kommer de tettere og tettere for ham. Kan det likevel stemme at de kommer s?pass hyppig p? slutten? Vi ser fra likning (6) at n?r \(r \rightarrow 2M\), g?r \(d\tau \rightarrow 0\). Tiden Wen m?ler mellom hvert lyssignal blir alts? kjempeliten faktor ganget med tiden idet han n?rmer seg eventhorisonten. Etterhvert vil han se lyssignalene mine med kortere mellomrom enn jeg sendte dem ut med... Noe er rart her, og det skal vi utforske videre i neste del.
Hva har vi funnet ut?
Jeg h?per du fortsatt henger med! S? langt har vi funnet ut n?r Wen i sitt romskip faller fritt inn mot det sorte hullet, mens jeg holder meg ved en planet som g?r i bane rundt det, blir Wens lyssignaler r?dforskyves p? vei til meg, mens mine bl?forskyves p? vei til ham. Jeg observerer at lyssignalene hans kommer treigere, mens han observerer at mine kommer tettere. Veldig tett. N? m? vi ikke glemme at vi hele tiden har antatt at lyset har uendelig fart. N? er det p? tide ? dykke litt dypere. Hvilke av resultatene v?re vil endre seg dersom vi tar hensyn til dette? Bli med videre og finn ut!
