IN-KJM1900 - H?st 2018

Beregninger og kjemi

IN-KJM1900, Andre forelesning, 23.oktober

Mål for økta:

  • Praktisk info
  • Ny syntaks:
    • Kodestruktur: moduler
    • Datastruktur: dictionaries
    • (Innlesing av r?data)
  • Ny teori:
    • Numerisk derivasjon
    • Newtons metode
    • Rekurrensrelasjoner/differensligninger

Moduler i Python

  • En modul er en samling med definisjoner lagret i en .py-fil.
  • En modul kan importeres i en annen fil med et import-statement:
In [13]:
from numpy import random   #importer "tilfeldige-tall-modulen" fra numpy

print(random.uniform(0,1,10)) #skriv ut 10 tilfeldige tall fra 0 til 1

[ 0.98460348  0.97262505  0.22300681  0.10491515  0.37354146  0.132127
  0.52865355  0.26977076  0.1273423   0.29544853]
In [23]:
import numpy as np #importer numpy og gi den et navn "np"

print(np.random.randint(0,6,10)) #skriv ut 10 tilfeldige tall fra 0 til 6

[3 5 3 3 2 3 2 0 1 2]

Moduler i Python

I eksempelet under lages en modul som importeres rett etterp?:

In [11]:
modfile = """
def really_important_reminder(name):
    print("Beware of asteroids, %s. They tend to collide." % name)
""" # A string to be stored as a module

file = open("reminder_module.py", "w") # open a file to write my modfile in
file.write(modfile) #write to file
file.close() #close file
In [12]:
import reminder_module as rm #importer modulen vi laget over

rm.really_important_reminder("Audun") #vis at det fungerer

Beware of asteroids, Audun. They tend to collide.

Om du ?nsker ? legge en modul i en subfolder til arbeidsfolderen, kreves det at du lager en tom fil __init__.py i subfolderen. For eksempel fra terminalen:

>touch [subfolder_name]/__init__.py

Moduler:

  • gir ryddigere kode.
  • er enklere ? vedlikeholde (enn sekvensiell kode).
  • er enklere ? erstatte og oppdatere.
  • legger til rette for gjenbruk.
In [60]:
from __future__ import solve_all_my_problems

  File "<ipython-input-60-d546266d3245>", line 1
    from __future__ import solve_all_my_problems
                                                ^
SyntaxError: future feature solve_all_my_problems is not defined

$\rightarrow$ Live kodeeksempel: "labtools.py"

Datastruktur: dictionaries

  • Dictionaries ( dict ) er sekvenser av data indeksert med valgfrie datatyper: keys
  • ...i motsetning til list og np.array som indekseres med heltall.

Eksempel:

In [73]:
H = {"name":"Hydrogen (H)", 
     "mass":1.008,
     "electrons": 1,
     "atomic number": 1} # Dicts are defined with curly brackets

print("Mass of hydrogen:", H["mass"]) #print mass of hydrogen

Mass of hydrogen: 1.008
In [71]:
# Create 3 dicts with alien movies:

alien1 = {"name":"Alien",
          "director": "Ridley Scott"}

alien2 = {"name":"Aliens",
          "director": "James Cameron"}

alien3 = {"name":"Alien 3",
          "director": "David Fincher"}


alien_movies = [alien1, alien2, alien3] #list of alien movie dicts

#iterate over all movies, print  name and director
for i in alien_movies:
    print("Movie   :", i["name"])
    print("Director:", i["director"])
    print(" ") #for separation

Movie   : Alien
Director: Ridley Scott
 
Movie   : Aliens
Director: James Cameron
 
Movie   : Alien 3
Director: David Fincher

En dict kan benytte ulike "keys"

In [79]:
my_dict = {"key1":1.000,
           2:"two",
           list:np.array([3])}

print(my_dict[list]) 

[3]

Dette kan v?re forvirrende. Tenk over: Kan du se for deg situasjoner hvor dette er nyttig?

Dictionaries: fordeler og ulemper

  • Enkle ? gj?re oppslag i
  • Trege ? gj?re oppslag i
  • Fleksibilitet i valg av "key" og "values"

$\rightarrow$ Live kodeeksempel: eksperimentsamling

"Focus, Daniel-san... focus"

Numerisk Derivasjon

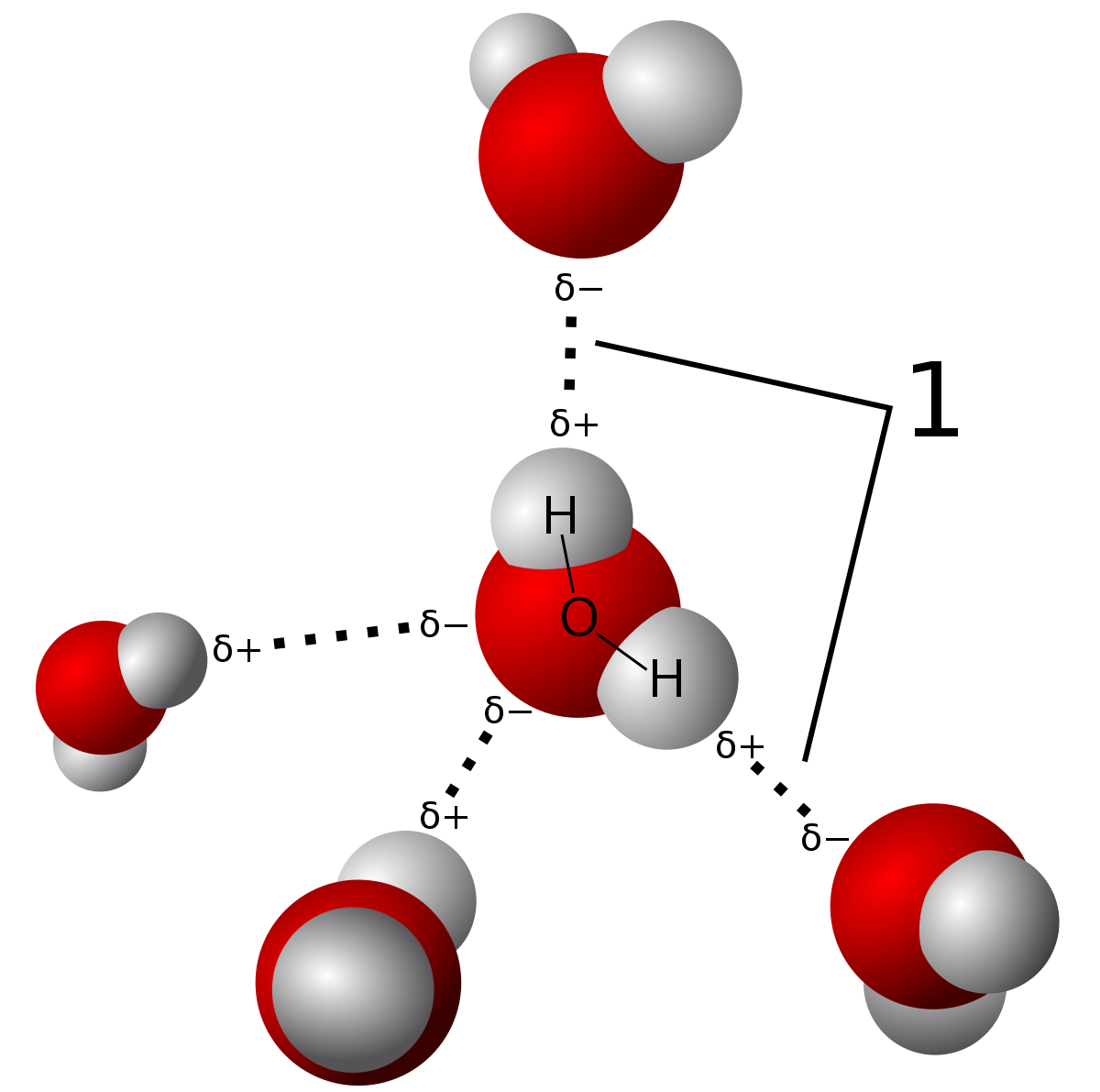
$$-\frac{d}{dx} U(x) = F$$

Kraften som virker p? en ladning fra et molekyl kan bestemmes ved ? derivere det elektrostatiske potensialet til molekylet med hensyn p? rom. (Bildet viser intermolekyl?re hydrogenbindinger (dipol-dipol) og er hentet fra Wikipedia)

Derivasjon

  • Derivasjon (og integrasjon) er helt sentrale konsepter i naturvitenskap.
  • Den deriverte er et m?l p? endringen i en funksjon $f(x)$ som f?lge av en endring i funksjonens variabel $x$.
  • I kjemi dukker derivasjon opp blant annet i:
    • dataprosessering
    • modellering
    • beregninger
    • reaksjonskinetikk
    • termodynamikk
    • kvantekjemi

Analytisk derivasjon

Den deriverte av en funksjon $f(x)$ er definert ved

$$ \frac{d}{dx} f(x) := \lim_{\Delta x \rightarrow 0} \frac{f(x + \Delta x) - f(x)}{\Delta x}$$

Du vil sannsynligvis m?te ulike ekvivalente skrivem?ter/notasjoner:

$$ \frac{d}{dx}f(x) = f'(x) = \dot{f}(x)$$

Numerisk derivasjon

Vi lar $\Delta x$ anta en endelig, liten verdi og ser vekk fra grensen:

$$ \mathbf{D}^+ f(x_0) := \frac{f(x_0 + \Delta x) - f(x_0)}{\Delta x}$$,

hvor vi har introdusert en forenklet notasjon for endelige differanser med operatoren $\mathbf{D}^+$.

$\rightarrow$ Eksempel

Numerisk derivasjon

Merk deg at vi evaluerer den deriverte i diskrete punkter langs x-aksen. For et gitt punkt $x_n$ er

$$ \mathbf{D}^+ f(x_n) := \frac{f(x_n + \Delta x) - f(x_n)}{\Delta x} := \frac{f_{n+1} - f_n}{\Delta x}$$

Denne m?ten ? bruke subindekser ($x_{\text{subindex}}$ ) p? for ? beskrive diskretisering er veldig nyttig og vil v?re standard gjennom kurset:

$$x \rightarrow x_n := x_0 + n \Delta x$$

$$ f(x_n) := f_n $$

Med "diskretisering" mener vi at vi kun har definerte verdier i noen f? punkter, verdiene utenfor punktene inng?r ikke.

Noen approksimasjoner p? den deriverte

Uttrykk Navn/sekant Operator
$\mathbf{D}^+ f(x) := \frac{f(t + \Delta t) - f(t)}{\Delta t}$ "Fremad-differanse" $\mathbf{D}^+$
$\mathbf{D} f(x) := \frac{f(x+ \Delta x) - f(x-\Delta x)}{2 \Delta x}$ "Senterdifferanse" $\mathbf{D}$
$\mathbf{D}^- f(x) := \frac{f(x) - f(x-\Delta x)}{\Delta x}$ "Bakoverdifferanse" $\mathbf{D}^-$

Disse definisjonene vil v?re spesielt nyttige n?r vi senere skal se p? numerisk l?sning av differensialligninger.

Kan T-Rex kun se bevegelser?

Fra Jurassic Park (1993)

$\rightarrow$ Live kode-eksempel

Eksempel (ikke pensum): dobbeltderivert

Vi kan bruke operatorene for ? finne uttrykk for den dobbeltderiverte i et punkt $x_n$, i dette tilfellet senterdifferansen

\begin{equation} \left( \frac{d}{dx} \right)^2 f(x_n) = f''(x_n) \approx \mathbf{D}_x \mathbf{D}_x f(x_n) \end{equation}

Om vi lar operatoren $\mathbf{D}_x$ virke p? $f(x_n)$ finner vi at

\begin{equation} \mathbf{D}_x \mathbf{D}_x f(x_n) = \mathbf{D}_x \frac{f(x_n+\Delta x) - f(x_n-\Delta x)}{2 \Delta x} = \frac{\mathbf{D}_x f(x_n+\Delta x) - \mathbf{D}_x f(x_n-\Delta x)}{2 \Delta x}= \frac{f(x_n+2\Delta x) - 2 f(x_n) + f(x_n-2\Delta x)}{4 \Delta x^2} \end{equation}

Siden $\Delta x$ bare er et vilk?rlig lite steg kan vi kalle den $2 \Delta x := \Delta \tilde{x}$ slik at

\begin{equation} \mathbf{D}_x \mathbf{D}_x f(x_n) = \frac{f(x_N+\Delta \tilde{x}) - 2 f(x_n) + f(x_n-\Delta \tilde{x})}{\Delta \tilde{x}^2} := \frac{f_{n+1} - 2 f_n + f_{n-1}}{\Delta \tilde{x}^2} \end{equation}

Hva om vi hadde h?rt i differanser?

Tenk over: hvordan tror du den deriverte av et lydsignal h?res ut?

$\rightarrow$ Praktisk lytteeksempel
Ikke pensum, men ganske interessant:

I musikkproduksjon benyttes ofte en effekt som kalles "high-pass-filter", som fjerner bass under en gitt frekvens.

(Bilde fra Wikipedia)

Denne kretsen kan modelleres med en s?kalt f?rste ordens ordin?r differensialligning, som involverer en f?rste ordens derivert.

Newtons metode

R?tter

Newtons metode er en fremgangsm?te som for en hvilken som helst jevn funksjon $f(x)$ lar oss finne en $x_*$ slik at

$$f(x_*) = 0$$

Disse punktene kalles r?ttene til funksjonen $f(x)$.
Vi kan konstruere et polynom slik at vi vet hvor r?ttene $x_0, x_1, x_2, ..., x_N$ er:

$$ f(x) = (x-x_0)(x-x_1)(x-x_2) ... = \Pi_i^N (x-x_0)$$

Dette kan v?re nyttig for ? teste funksjoner i prosjektoppgaven.
I et hvilket som helst punkt $x_n$ kan vi beregne en tangent $t_f(x)$. Uttrykket for tangenten er

$$ t_f(x) = f(x_n) - f'(x_n)(x-x_n) $$

I dag har dere ogs? l?rt ? regne den numerisk:

$$ t_f(x) \approx f(x_0) - \mathbf{D}^+f(x_0)(x-x_0) $$
I et gitt punkt $x_n$ kan vi finne tangentens rot $t_f(x_{n+1})=0$ ved ? l?se ligningen

$$ t_f(x_{n+1}) = f(x_{n}) - f'(x_{n})(x_{n+1}-x_{n}) = 0$$

L?ser vi ligningen over for $x_{n+1}$ finner vi med enkel algebra at

$$ x_{n+1} = x_{n} - \frac{f(x_n)}{f'(x_n)}$$

Tenk igjennom:

Leder tangenten deg n?rmere en $x_*$-verdi hvor $f(x_*) = 0$?

Hvor leder tangenten n?r $f'(x_i) = 0$?

Hva skjer n?r tangenten leder deg gjennom en rot? Hvor vil neste beregnede tangent ta deg?

Beskrivelse av Newtons metode

Newtons metode er en fremgangsm?te/algoritme som for en hvilken som helst jevn funksjon $f(x)$ lar oss finne en $x_*$ slik at $$f(x_*) = 0$$ Den formelle beskrivelsen er at vi f?rst gjetter p? en $x_0$, og deretter gjentar f?lgende operasjon $$ x_{n+1} = x_{n} - \frac{f(x_n)}{f'(x_{n})}$$ Vi gjentar frem til enten et maksimalt antall interasjoner er n?dd, eller at forskjellen mellom $x_n$ og $x_{n+1}$ er mindre enn en grenseverdi: $$ \vert x_n - x_{n+1} \vert \le \epsilon$$

Dette kalles en konvergensbetingelse.

$\rightarrow$ Vi ser p? et interaktivt eksempel

Oppsummering av dagen:

  • Ny syntaks:
    • Kodestruktur: moduler
    • Datastruktur: dictionaries
    • Innlesing av r?data
  • Ny teori:
    • Numerisk derivasjon
    • Newtons metode

Takk for i dag

Slides vil bli lagt ut på semestersidene.